Let \(x_1, x_2, x_3\) be three points in a plane. We define \(x_4\) the point on the ray \([x_3 x_1)\) located at a distance \(1\) of \(x_3\). It is as \(x_1\) has been attracted to \(x_3\) but kept at distance. We continue by defining \(x_5\) the point on the ray \([x_4 x_2)\) located at a distance \(1\) of \(x_4\).

On the whole, we define from \((x_1, x_2, x_3)\) a recurrent sequence taking values in \(\mathbb{R}^2\) and such that, for \(n \geq 4\) (with \(N: x \mapsto \frac{x}{\| x \|}\) where \(\|.\|\) is a norm):

\[x_{n} = x_{n-1} - N(x_{n-1} - x_{n-3}).\]

We would like to study how behaves this sequence for large \(n\).

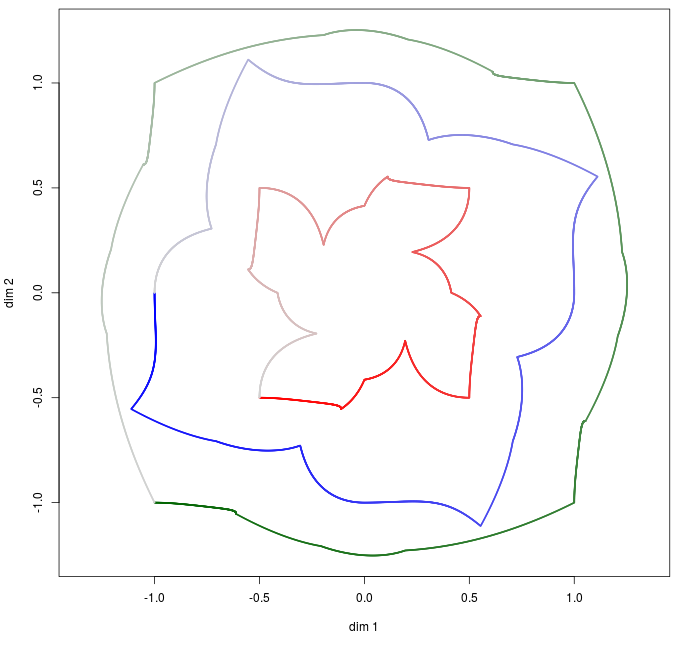
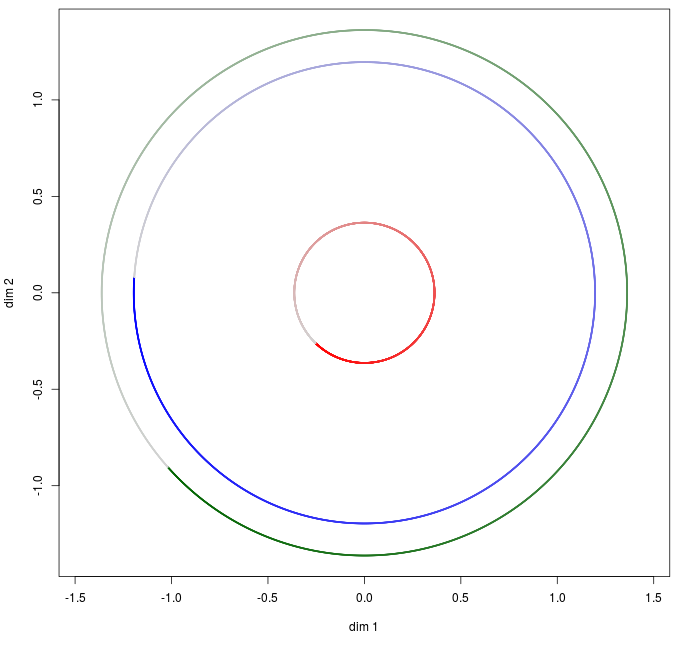
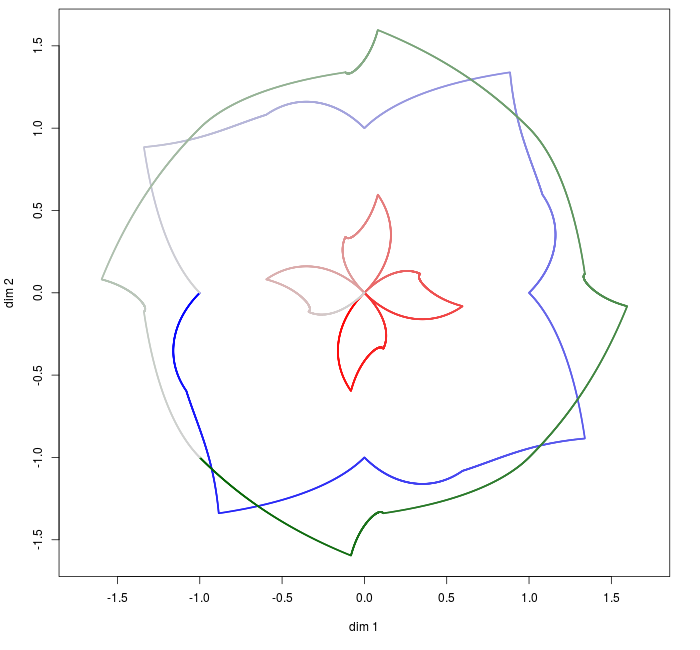
Fig. 1. Illustration (see Fig. 11 for details)

Except for the last part of this post, we select the Euclidian norm and identify the plane with the complex plane.

Understanding the recurrence on an example

We illustrate the first steps of the sequence when \(x_1=(0,0)\), \(x_2=(1,0)\), and \(x_3=(1,1)\). The construction of \(x_4\) is shown in Fig. 2. This can be computed from the formula:

\[x_{4} = x_{3} - N(x_{3} - x_{1}) = (1,1) - N((1,1)) = (1 - 1/\sqrt{2}, 1 - 1/\sqrt{2}).\]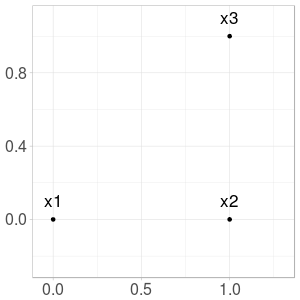

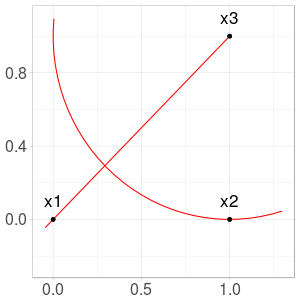
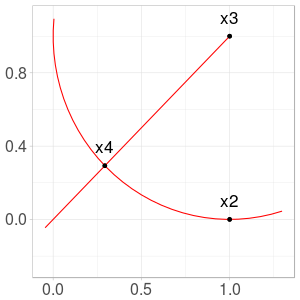
Fig. 2. Construction of \(x_4\) from \(x_1\) and \(x_3\)

Next points \(x_5\) and \(x_6\) are more difficult to calculate from the formula, and we only provide the construction (Fig. 3 and 4).

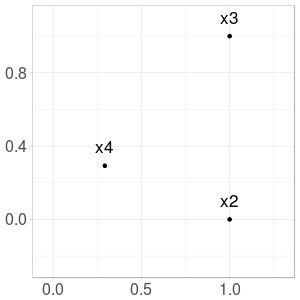
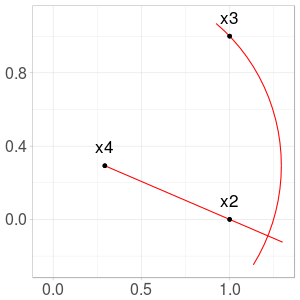
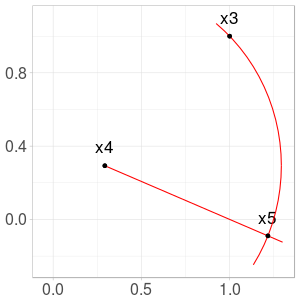
Fig. 3. Construction of \(x_5\) from \(x_2\) and \(x_4\)

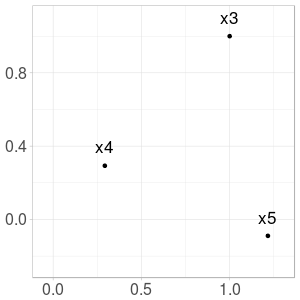
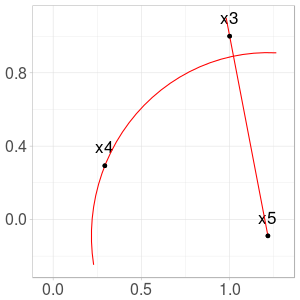
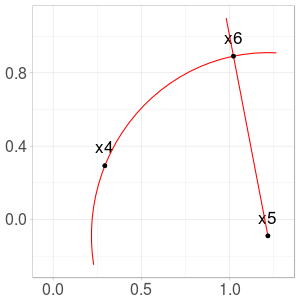
Fig. 4. Construction of \(x_6\) from \(x_3\) and \(x_5\)

After some steps, we obtain \(3\) adherent points forming an equilateral triangle. Initial and final steps are shown in Fig. 5.

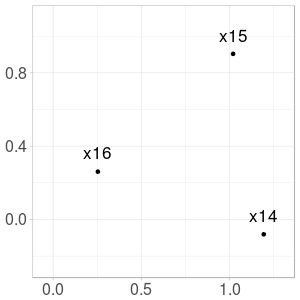
Fig. 5. Initial and final steps

Note that the sequence may be undefined for some initial triplets (for example when \(x_1 = x_2 = x_3\)).

Reducing dimension of the problem

Each triplet contains \(6\) real parameters. We will show that we can reduce the triangle pursuit problem to \(1\) parameter without loss of generality. Explicitly, our final parameter will be \(t \in (0, 2 \pi) \setminus \lbrace \pi \rbrace\), related with triplet \((x_1, x_2, x_3) = (0, 1, e^{it})\). Calculations are tedious, so you can skip them at first reading.

Applying rotation and translation

Suppose that \((x_n)_n\) is well-defined from triplet \((x_1, x_2, x_3)\). Let \(\theta \in [0, 2 \pi)\) and \(b \in \mathbb{C}\). Let for \(k \in \lbrace 1, 2, 3 \rbrace\): \(x'_k := e^{-i \theta} (x_k - b).\)

Then, for \(k \in \lbrace 1, 2, 3 \rbrace\), \(x_k = e^{i \theta} x'_k + b.\) We rewrite \(x_4\) as follows:

\[x_4 = x_3 - N(x_3 - x_1) = e^{i \theta} x'_3 + b - N(e^{i \theta} x'_3 - e^{i \theta} x'_1).\]

Because \(N(.)\) is defined with the Euclidian norm, we obtain:

\[x_4 = e^{i \theta} x'_3 + b - e^{i \theta} N( x'_3 - x'_1) = e^{i \theta} \left(x'_3 - N( x'_3 - x'_1) \right) + b.\]

Since \(x_4\) exists, \(x'_3 - N( x'_3 - x'_1)\) exists and we define: \(x'_4 := x'_3 - N( x'_3 - x'_1).\)

We can continue and define \((x'_n)\) such that for all \(n\): \(x'_n := e^{i \theta} x'_n + b.\)

From 6 to 3 parameters

Suppose as before that \((x_n)_n\) is well-defined from triplet \((x_1, x_2, x_3)\).

Rotation and translation have released \(3\) degree of freedom. In this paragraph, we select \(\theta\) and \(b\) to obtain a triplet \((x'_1, x'_2, x'_3)\) verifying those \(3\) conditions:

\[x'_1 \text{ on the ray } ]x'_3 0)~~~;~~~x'_2 \in \mathbb{R}^{+}~~~;~~~\| x'_3 \| = 1.\]

Positions of \(x'_1, x'_2, x'_3\) are illustrated in Fig. 6.

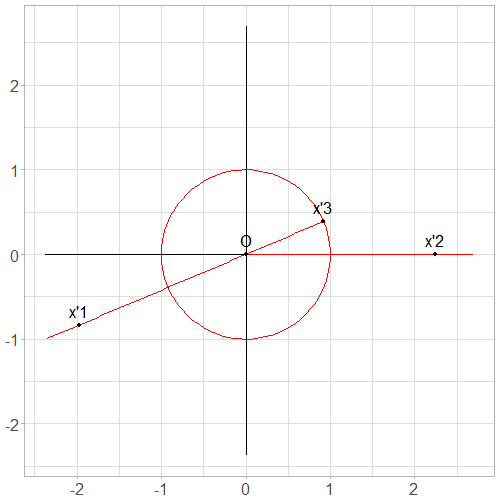
Fig. 6. Typical positions of \(x'_1, x'_2\) and \(x'_3\) after transformation

First, we have \(x_3 \neq x_1\), otherwise \(x_4\) cannot be defined. Then, we let:

\[s:= \text{Arg}(x_3 - x_1) \in [0, 2 \pi),\] \[r:= 1 - \| x_3 - x_1 \| \in (-\infty, 1),\] \[A \geq 0 \text{ and } t \in [0, 2 \pi) \text{ such that } A e^{-it} := 1 + (x_2 - x_3)e^{-is}.\]

We select:

\[\theta := s - t,\] \[b:= x_3 - e^{is}.\]

We compute \(x'_1, x'_2, x'_3\):

\[x'_1 = e^{-i \theta}(x_1 - b) = e^{-i s}e^{i t}(x_1 - x_3 + e^{is}) = e^{-i s}e^{i t}(-(1-r) e^{is} + e^{is}) = r e^{it}.\] \[x'_2 = e^{-i \theta}(x_2 - b) = e^{-is}e^{it}(x_2 - x_3) + e^{it} = e^{it} (1 + (x_2 - x_3) e^{-is}) = A.\] \[x'_3 = e^{-i \theta}(x_3 - b) = e^{-is}e^{it}e^{is} = e^{it}.\]

\(x'_1, x'_2, x'_3\) verify the \(3\) conditions, so the conclusion.

From 3 to 1 parameters

We consider \((x'_1, x'_2, x'_3)\) as is the last paragraph.

From the recurrence relation, we obtain: \(x'_4 = 0\) regardless of \(r\). The term \(x'_1\) is not used for subsequent terms, so we can let \(r = 0\) and consider \((x''_1, x''_2, x''_3) = (0, x'_2, x'_3).\)

Then, we observe that \(A \neq 0\), otherwise \(x''_5\) cannot be defined. From the recurrence relation, we obtain: \(x''_5 = 0\) regardless of remaining \(A\). The term \(x''_2\) is not used for subsequent terms, so we can let \(A = 1\) and consider \((x'''_1, x'''_2, x'''_3) = (0, 1, e^{it}).\)

This construction is illustrated in Fig. 7.

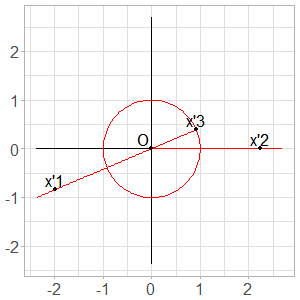
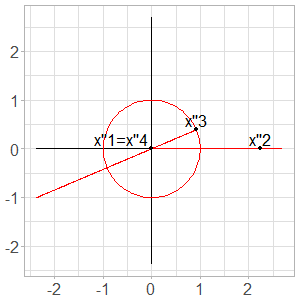
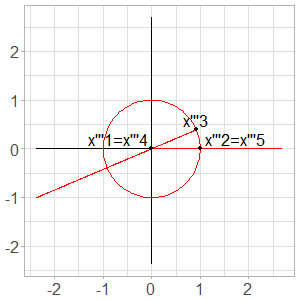
Fig. 7. From \(3\) parameters to \(1\) parameter

We have reduced the problem to \(1\) dimension without loss of generality. We observe that parameters \(t = 0 \text{ mod } \pi\) are impossible. We are now interested to understand the behavior of the sequence as a function of \(t\).

Formula for \(x_n\)

In this section, we let \(t \in (0, \pi)\) and \((x_1, x_2, x_3) := (0, 1, e^{it})\).

First terms are easy to compute:

\[x_4 = 0,~~~x_5 = 1.\]

After that, I follow indication provided by achille hui here.

Let \(u_n = x_{n} - x_{n-1}\) for \(n \geq 2\). \(u_n\) represents the vector from \(x_{n-1}\) to \(x_n\). For \(n \geq 4\), we have \(\|u_n\| = 1\). So for \(n \geq 5\), there exists \(\theta_n\) such that \(e^{i \theta_n} = u_n / u_{n-1}\). \(\theta_n\) represents the angle between \(u_{n-1}\) and \(u_{n}\).

For \(n \geq 5\), we observe that triangle \((x_{n-2}, x_{n-1}, x_n)\) is isocele with angles \(\pi - \theta_n\), \(\pi - \theta_{n+1}\) and \(\pi - \theta_{n+1}\) (see Fig. 8 for details). It follows \(\pi = \pi - \theta_n + 2(\pi - \theta_{n+1})\) i.e. \(\theta_{n+1} = \pi - (1/2) \theta_n.\)

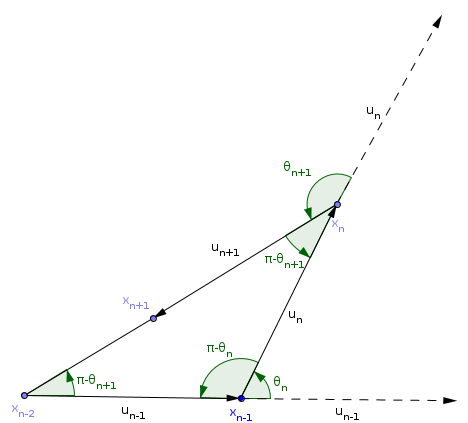
Fig. 8. Angles in triangle \((x_{n-2}, x_{n-1}, x_n)\)

After some calculations, we get for \(n \geq 5\):

\[x_n = \sum_{k=0}^{n-5} e^{\frac{2ik \pi}{3}} e^{\frac{i}{3}\left( t - \frac{\pi}{3} \right) \left[ 1 - \left(-\frac{1}{2} \right)^k \right]}.\]

[this formula in only valid in the interval \((0, \pi)\)].

Adherent points

For each \(t \in (0, 2 \pi) \setminus \lbrace \pi \rbrace\) and \((x_1, x_2, x_3) := (0, 1, e^{it})\), we observe that \((x_n)_n\) has \(3\) adherent points forming an equilateral triangle.

We map each initial triplet to the corresponding adherent points.

We show in Fig. 9 the mapping from \((0, 2 \pi) \setminus \lbrace \pi \rbrace\) to the corresponding adherent points. Images of components \((0, \pi)\) and \((\pi, 2 \pi)\) are symmetric with respect to the x-axis.

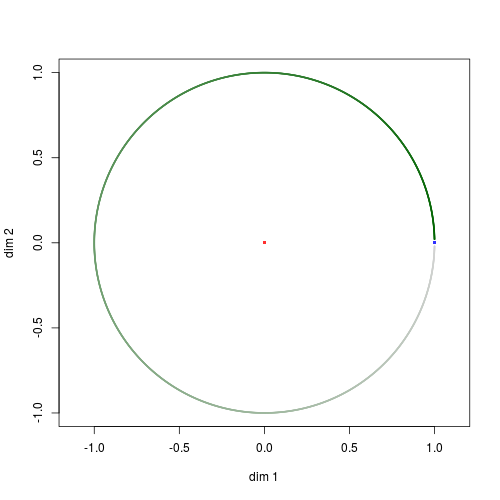
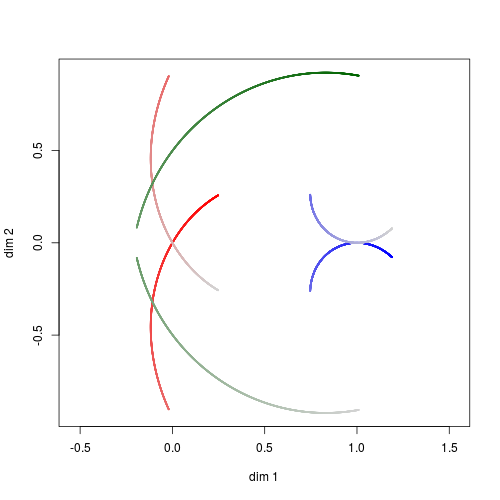
Fig. 9. Mapping from \((0, 2 \pi) \setminus \lbrace \pi \rbrace\) (left) to the corresponding adherent points (right). Bright colors correspond to small values of \(t\), and faded colors to larger values.

We restrict the mapping on the interval \((0, \pi)\) and show a more detailed plot in Fig. 10. Notice that triangle corresponding to \(t = \pi / 3 \approx 1.05\) remains unchanged by the mapping.

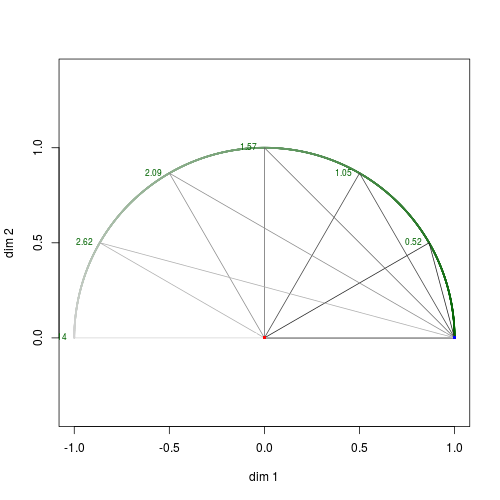
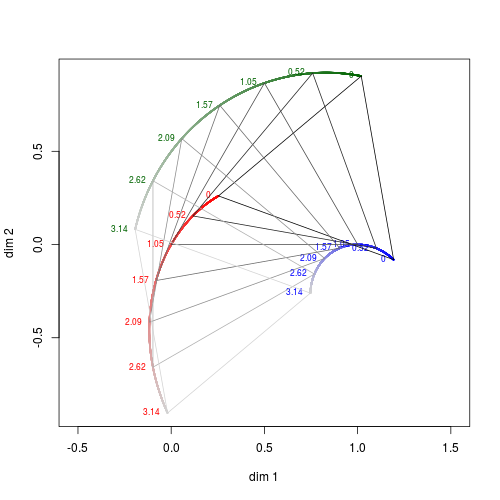
Fig. 10. Mapping from \((0, \pi)\) (left) to the corresponding adherent points (right).

Illustration with other norms

Let \(x_1=(0,0)\), \(x_2=(1,0)\), and \(x_3=(1,1)\).

Map of a rotation

We are interested to see mapping of \(e^{i \theta}(x_1, x_2, x_3)\) for \(\theta \in (-\pi, \pi)\).

When \(\|.\|\) is the Euclidian norm, we already know the global behavior. But with one-norm or maximum norm, strange figures are obtained. Those mappings are depicted in Fig. 11.

Fig. 11. Mapping from \(e^{i \theta}(x_1, x_2, x_3)\) to the corresponding adherent points for one-norm, Euclidian norm and maximum norm respectively.

Map of an homothety

We are interested to see mapping of \(\theta \times (x_1, x_2, x_3)\) for \(\theta \in (-\pi, \pi)\).

The mappings are depicted in Fig. 12.

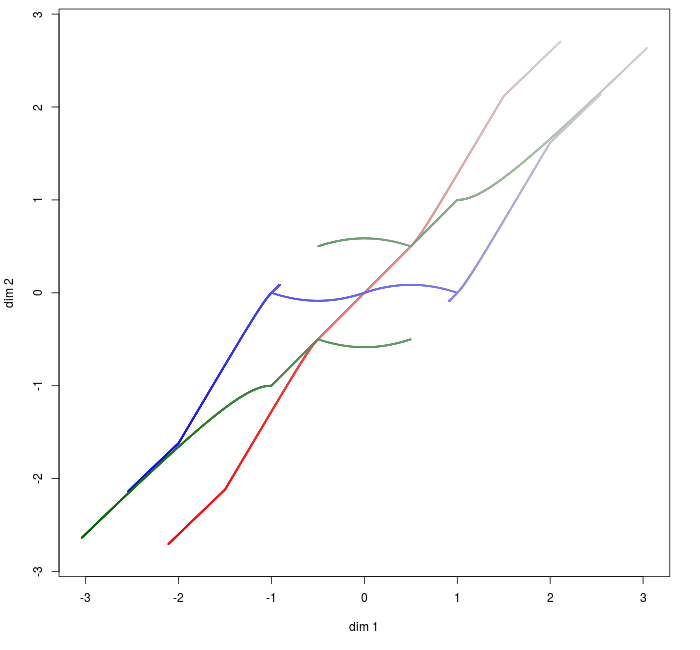
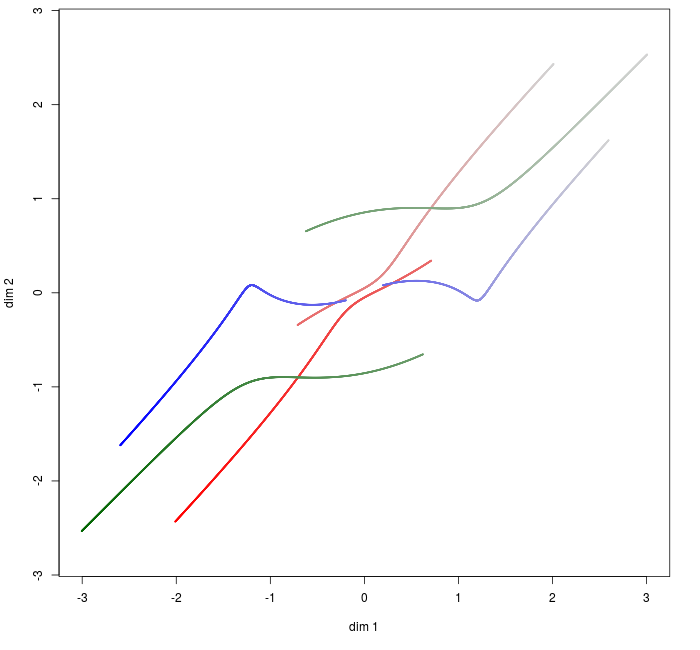
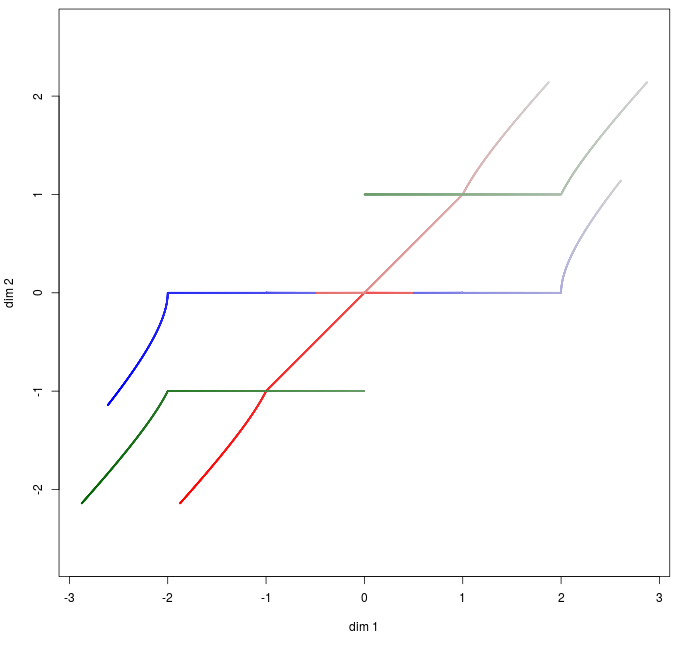
Fig. 12. Mapping from \(\theta \times (x_1, x_2, x_3)\) to the corresponding adherent points for one-norm, Euclidian norm and maximum norm respectively.

References

• Code is available on my github. Many examples are provided, and code contains some generalization with more initial points, higher dimension, etc.
• I wrote a question in math.stackexchange asking about the asymptotic behavior of \((x_n)_n\). Thanks for achille hui for his comment.