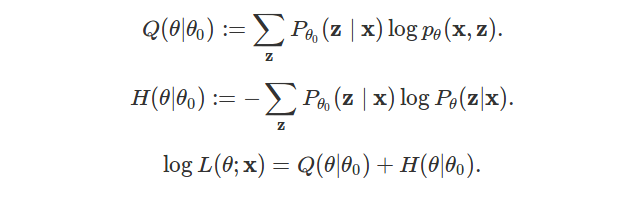maths and data
Let \(f\) be a real function. For \(\lambda > 0\), we are interested in the equally-spaced summation \(\sum_{k=-\infty}^{+\infty} f(.+k\lambda)\), that can be interpreted depending on the context as a periodic mixture or as a wrapped distribution. For some specific functions such as the Gaussian density, we derive expressions, evaluations, and approximations of the sum, further accompanied with visualization of the different shapes for various values of \(\lambda\).
Let \(Z\) be a \(\text{Exp}(1)\) random variable. For \(\alpha_1, \ldots \alpha_N \in \mathbb{R}_{+}^{*}\), we are looking for variables \(X_1, \ldots X_N\) independent and following the same distribution such that:
\[Z = \sum_{j=1}^{N} \alpha_j X_j.\]For the special case where all \(\alpha_j\) are equal, this corresponds to the problem of infinite divisibility of the exponential distribution, and in this case \(X_1\) follows \(\text{Gamma}(1/N, 1/\alpha_1)\), a gamma variable with shape \(1/N\) and scale \(1/\alpha_1\) (in particular when \(N=1\), we have \(X_1 \sim \text{Exp}(\alpha_1) = \text{Gamma}(1, 1/\alpha_1)\)).
We are willing to extend this divisibility property by deriving the characteristic function of \(X_1\) before inversing it numerically to retrieve the density. Some visualizations are provided.
This tutorial highlights structure of common RNN algorithms by following and understanding computations carried out by each model. It is intended for anyone knowing the general deep learning workflow, but without prior understanding of RNN. If you really never heard about RNN, you can read this post of Christopher Olah first.
The present post focuses on understanding computations in each model step by step, without paying attention to train something useful. It is illustrated with Keras codes and divided into five parts:
[This tutorial has been written for answering a stackoverflow post, and has been used later in a real-world context].
This tutorial provides a complete introduction of time series prediction with RNN.
In part A, we predict short time series using stateless LSTM. Computations give good results for this kind of series.
In part B, we try to predict long time series using stateless LSTM. In that case, model leads to poor results.
In part C, we circumvent this issue by training stateful LSTM. Stateful models are tricky with Keras, because you need to be careful on how to cut time series, select batch size, and reset states. I wrote a wrapper function working in all cases for that purpose.
In part D, stateful LSTM is used to predict multiple outputs from multiple inputs.
Coal is a small software dedicated to automatize composition of linear functions. For example, it can compute slope, intercept and fixed point of gfg given f: x ↦ ax+b and g: x ↦ cx+d. Here, a and b can be formal letters, rational values or real values.
Let \(x_1, x_2, x_3\) be three points in a plane. We define \(x_4\) the point on the ray \([x_3 x_1)\) located at a distance \(1\) of \(x_3\). It is as \(x_1\) has been attracted to \(x_3\) but kept at distance. We continue by defining \(x_5\) the point on the ray \([x_4 x_2)\) located at a distance \(1\) of \(x_4\).
On the whole, we define from \((x_1, x_2, x_3)\) a recurrent sequence taking values in \(\mathbb{R}^2\) and such that, for \(n \geq 4\) (with \(N: x \mapsto \frac{x}{\| x \|}\) where \(\|.\|\) is a norm):
\[x_{n} = x_{n-1} - N(x_{n-1} - x_{n-3}).\]We would like to study how behaves this sequence for large \(n\).
Many methods exist to visualize high-dimensional data through a two-dimensional map. Those include linear techniques such as PCA and MDS; as well as nonlinear ones such as Isomap, LLE, SNE and t-SNE (resp. Principal Component Analysis, 1933; MultiDimensional Scaling, 1952; Isomap, 2000; Locally Linear Embedding, 2000; Stochastic Neighbor Embedding, 2002; t-Distributed Stochastic Neighbor Embedding, 2008). Some of those dimensionality reduction methods are illustrated in this sklearn example.
A popular method for nonlinear mapping is t-SNE. This method has been developed by Laurens van der Maaten and Geoffrey Hinton in [1]. It is based on SNE and improves it by addressing the “crowding problem” (tendency of mapped points to aggregate into a unique central cluster). You can familiarize yourself with t-SNE here, which allows exploration of various examples interactively.
In this post, we propose to derive gradient of the SNE algorithm (not to be confused with t-SNE, for which gradient calculation is detailed in Appendix A of [1]). SNE gradient is given in both original and t-SNE article, but neither detailed (see Equation 5 of [2], and Section 2 of [1]).
This post explains why maximizing likelihood is equivalent to minimizing KL-divergence. This can already be found here and here, but I restate this in my “own” words.
More generally, I encourage you to read Section 3.13 of Deep Learning book for insights on information theory.
Let \(\mathbf{x} = (x_1, \ldots x_n)\) a dataset of \(n\) elements.
We assume that each \(x_i\) has been sampled independently from a random variable \(X\) with density \(p = p_{\theta_0}\) and corresponding to a true (unknown and fixed) parameter \(\theta_0\).
We let \(q = p_{\theta}\) the density function corresponding to another parameter \(\theta\).
The likelihood of \(\mathbf{x}\) given \(\theta\) is \(L_{\theta}(\mathbf{x}) = \prod_{i = 1}^n p_{\theta}(x_i)\).
The opposite of log-likelihood divided by \(n\) is:
\[-\frac{1}{n} \log L_{\theta}(\mathbf{x}) = -\frac{1}{n} \sum_{i=1}^n \log p_{\theta}(x_i) \xrightarrow[n \rightarrow +\infty]{} E_{\theta_0} \left[ - \log p_{\theta}(X) \right],\]and
\[E_{\theta_0} \left[ - \log p_{\theta}(X) \right] = - \int \log p_{\theta}(x) dp_{\theta_0}(x) = - \int \log q(x) dp(x) =: H(p, q).\]In the previous equation, \(H(p, q)\) stands for the (continuous) cross-entropy between \(p\) and \(q\). We let \(H(p)\) the (continuous) entropy of \(p\) and \(\text{KL}(p \mid \mid q)\) the Kullback-Leibler divergence between \(p\) and \(q\).
Since \(H(p, q) = H(p) + \text{KL}(p \mid \mid q)\), maximizing likelihood is equivalent to minimizing KL-divergence.
A Gaussian Mixture Model (GMM) models data as a finite mixture of Gaussians. It is often used to perform clustering. In this case, the number of Gaussians \(K\) is the number of clusters and is initially selected. Compared to \(K\)-means, GMM allows clusters with uneven variance and density.
Parameters are usually estimated using an Expectation-Maximization (EM) algorithm, its aim being to iteratively increase likelihood of the dataset. GMM is actually a perfect model to understand how EM is working.
Expectation-Maximization algorithm (EM) is an algorithm used to estimate parameters of statistical models comprising latent variables. It is applied in the case where direct calculation of maximum likelihood estimation (MLE) is impractical. EM updates parameters of the model iteratively, in order to increase likelihood of the set. It generally gives good estimation results, although there is no guarantee of convergence to MLE.
Many introductions of EM exist on the web. This one starts from the likelihood computation problem and uses inductive reasoning to bring out EM. No implementation is provided.
We begin by describing a general model involving latent variables. We then explain why direct computation of MLE is intractable. After that, ideas are introduced one by one and lead us naturally towards EM. Those ideas are formalized afterwards, making EM a practical algorithm to estimate parameters.
Langton’s ant is a cellular automaton driven by a simple set of rules and running on a square lattice. It is one of the most simple system leading to an emergent behavior. In this post, the system is extended to run on any Voronoi tessellation of the plane. Simulations show interesting walks for some partitions of the plane, including chaotic structures, highway patterns and even bounded evolutions.
Metropolis–Hastings algorithm is a method for sampling from a probability distribution. It is used when direct sampling is difficult.
This post illustrates the algorithm by sampling from \(\mathcal{N}(. \mid > 5)\) – the univariate normal distribution conditional on being greater than \(5\). This example has been chosen for its simplicity, for understanding how the algorithm actually works.
For real applications, other methods are preferred for sampling \(\mathcal{N}(. \mid > l)\): It is direct for \(l = 5\), and more tricky when \(l\) is larger than \(10\). You can read this Wikipedia section for details.
Simulation code has been written in R and is available at that address.
In this post, we explore data collected with Anabasis webapp. 144674 records have been retrieved consisting of date, picture number, cell position and user id. We derive density plots from data to deduce where players prefer to click. Afterwards, we show how players share the work together on some selected pictures.
Anabasis is a webapp where players can draw collaborative paintings. Each draw stands on a board containing ten thousand cells. Every player contributes at the same time on the same drawing. When a player clicks on a dark cell, it transforms to a light cell.
The work is finished when one special cell among ten thousand has been found. At this moment, the lucky player can choose the name of the draw. Finished artworks are therefore available in the draws section.
Click on the screen to launch the game in your browser. The loading may take some seconds.
I released this webapp as a challenge to understand how node.js and mongodb are working. I deployed the app with Heroku and MongoLab. The whole source is available in my github! Analysis of data collected with the app is available here.
Bank vault holdup is a game where you have to guess a secret pass to open the bank vault and get the reward! There is no hint, you just have to follow your intuition.
Click on the screen to launch the game in your browser. The loading may take some seconds.
The Nim function for take-a-prime game is a math sequence with interesting patterns. We define this sequence \((u_n)\) recursively. For all \(n\) in \(\mathbb{N}\) (the set of non-negative integers), \(u_n\) is the lowest number in \(\mathbb{N}\) such that for all prime numbers \(p\) (with \(n-p \geq 0\)), \(u_n \neq u_{n-p}\).
Trigger snake is a snake game with new features, making it fast, lively and challenging. You can download it here (Windows), or compile C++/Qt4 sources yourself. The software contains a component to display graphical statistics in-game. It can be used to follow player’s behavior, for example by showing preference to some regions or directions.
Sikuli is a software controlling your keyboard/mouse devices in order to do some automatic tasks. It was initiated at MIT and is currently developed by Raimund Hocke. It works on all platforms and is available here.
In the sequel, I show an example to collect images from Google Maps and make a map from them. The aim is to draw a French island, l’île d’Oléron.
Those slides are an introduction to particle filters, with an homemade example of trajectory tracking. The presentation has been given in 2014 for the Colloque Inter’Actions 2014.
Source code of simulations are available on my github.
Here is my slides of a talk given for doctoral students in 2013. It is an introduction to hidden Markov models (on finite state spaces), following the tutorial of L. R. Rabiner.
Source code of simulations are available on my github.
How to make a 3×3×3 cube with six 2×2×1 cuboids and three 1×1×1 cubes, i.e. to show the following “equation”? You can move them, change their orientation, but splitting is not allowed.
Like other Romance languages, French nouns are divided in two almost distinct genders: feminine and masculine. Deciding the gender of a word is not obvious. For example, a table is feminine (“une table”) but an acid is masculine (“un acide”).
On the following plots, we check out the distribution of the gender across the letters. We then learn a simple tip to choose the gender of an unknown noun.
FlapMMO is an online game similar to Flappy Bird. The player controls a bird and the aim is to fly as far as possible, avoiding the pipes. At the same time, you see other players playing.
In this post, an exploration of a dataset of scores is performed, using descriptive statistics and testing some probabilistic models.
Using a computer cluster to run some program is useful if your program needs:
In those cases, you can follow this short tutorial, designed for the ICJ cluster.
What the Earth would look like if the sea level suddenly changed? And what would be the Moon, Mars and Venus with as much water as on the Earth? Show this on the following maps and compare our Earth with other astronomical objects.
World maps. On this first map, we can show how the
world would be if the sea level increased by +100m.
Could you find the missing symbol in the sequence shown below?
